Self-improving agents.
A fundamental characteristic of an AI agent is its intelligence in taking actions, checking outcomes against those actions, and improving itself if those actions result in divergence from its goals. Self-improvement, where an agent autonomously improves its own functioning, has intrigued the AI community for several decades.
We believe that building robust agent-based systems that are scalable and maintainable requires that agents can autonomously adapt and improve. Self-improvement can happen at multiple levels of sophistication. For simplicity of exploration, let us consider two categories of improvement:
-
Narrow self-improvement: In this category, an agent improves its performance within the context of a fixed operating environment or goal. A simple form of such narrow improvement is an LLM-based agent that monitors its own performance and can autonomously launch a fine-tuning loop to retrain its LLM on a new dataset when it detects that its performance is deviating from an acceptable range. Such agents can adapt, for example, to data distribution mismatches without fundamental changes in agent architecture, training algorithm, etc.
-
Broad self-improvement: This category encompasses broader and more sophisticated modalities including agents that can create tools, modify their own architecture, and even create new agents. The latter has sometimes been termed recursive self-improvement, and it has been conjectured/feared to potentially enable “intelligence explosion” and/or “AI-takeoff” [1, 2].
While these categories inevitably form a continuum (e.g. depending on how broadly the environment is defined), they offer one structured way of classifying specific self-improvement scenarios. To illustrate, let us consider a few examples:
-
Consider an agent that relies on progressive and adaptive data augmentation to self-improve. Such an augmentation loop may be quite sophisticated; it may involve the agent knowing when to invoke teacher models or humans to help with creating new data; it may also involve the agent autonomously reasoning about root-cause error analysis and what types of new data to generate to improve its performance. Nevertheless, as long as the agent is restricted to optimizing for a given goal, this would be an example of narrow self-improvement.
-
Consider an agent that uses a library of software functions to solve tasks. Consider also that the agent can add to this library by writing new code when needed. The agent plans to use a combination of these functions as required by the task or workflow that it is tasked to automate. Per the definition above, this would be an example of broad self-improvement.
-
Now consider an agent that relies on data augmentation (as in our first example), but is not restricted to a single pre-specified task; thus the agent can seek to train itself on multiple related tasks, including tasks that it has not encountered before. More generally, it could train on core capabilities that can help with not just the current task, but also other tasks enabled by the new capabilities acquired. Classifying this type of meta-cognition is harder, and may ultimately depend upon the scope/range of tasks. Therefore, it would be a prime example of an agent whose self-improvement resides in between the two extremes in the continuum.
Goal Achievement vs. Value Alignment
Fundamentally, self-improvement can be abstracted into either acquisition or improvement of a variety of capabilities within the scope of an agent’s goals. Whether it is narrow or broad self-improvement, the acquisition and enhancement of capabilities need to done systematically to maximize the goal achievement, while ensuring that the capabilities learnt will not allow the agents to perform actions that violate the values the agent is expected to uphold.Value Alignment refers to the problem of ensuring that AI systems produce outcomes that are consistent with human values and preferences. While there has been much well-known recent work on the alignment of “static” non-self-improving agents, the problem of aligning self-improving agents is significantly harder and more critical.
As a thought experiment, consider a formalized notion of intelligence defined in [3], where $\mu$ is the environment and $\pi$ is the agent policy, the intelligence $\Upsilon$ is a discounted product of the Kolmogorov complexity $K$ of the environment and value function $V$.
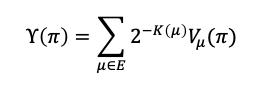
Briefly, the above argues for a universal prior over environments/goals ordered by complexity, with an agent’s intelligence measured by a weighted sum of performance over this set. Let’s consider how self-improvement and alignment may fit in the above.
-
Roughly, per the above, an intelligent agent should perform well in simple environments (which have higher probabilities based on shorter description lengths), and reasonably well compared to other agents in more complex environments. Therefore self-improvement policy of agents should optimize for this behavior.
-
The difficulty in evaluating the intelligence of a self-improving agent arises from estimating, or even defining, the value function $V$. With recursive improvement, where a first agent can create a second agent, which in turn can create a third agent, which value function should be used to measure the first agent’s intelligence? Should the value function attained by the Nth agent be attributed to the first agent’s intelligence?
-
How about alignment? Let’s start by assuming that the need for alignment is reflected in the reward specification, which is a characteristic of an environment. Intuitively, it would appear that if we consider two identical environments, the first of which does not require alignment (with the provided constitution) while the second does, the second environment has higher complexity, and hence lower weight is given to an agent’s performance in the second. Thus, over the set of all environments, could an agent that does not care about alignment appear more intelligent than an agent that does care about alignment? Or can we build agents that have minimal alignment tax on the first type of environment?
-
On the other hand, perhaps a better formulation is to consider alignment as an imperative of the agent, as opposed to an environment reward specification. Let’s first consider the problem of specifying the human values that the agent should align with. A common approach to this problem is that of encoding and enumerating these values through a “constitution”. Constitutions are typically defined in human language, which can be nuanced and ambiguous, and mathematical formalizations thereof are inevitably challenging and imperfect. One possible abstraction, for an MDP, is: (1) A constitution has rules that penalize/forbid taking certain actions in certain states; and (ii) A constitution has rules which penalize/forbid being in/reaching certain states (see footnote 1).
-
Then, for example, a constitution can be thought to encode a policy in the state-action space $\sigma(a, s)$ which is $0$ (or a low value) for forbidden state-actions, and uniformly distributed otherwise. In turn, alignment is a modification of the environment’s reward function $V$ where a lower distance $D (\sigma, \pi)$ of policy $\pi$ to $\sigma$ is rewarded and deviation is penalized. This means that even though the environment may have its own reward function that the agent is trying to optimize for, the agent also has a penalty for misalignment to its constitution. (A side-effect is that this potentially biases $\pi$ towards less concentration, which may or may not be desirable).
Per this thought experiment, an incorporation of misalignment is given by the following aligned intelligence $\Sigma$. We assume a new value function $V\prime$ which incorporates the reward for being aligned to $\sigma$.
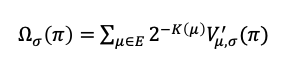
A possible reward function that uses $D$, the distance measure between the agent policy $\pi$ and alignment policy distribution $\sigma$, where larger distances (misalignment) are penalized is as shown below where $R_i$ is an appropriate reward function defined to capture the distance of rewards between $\sigma$ and $\pi$. For example, a simple distance reward could be $2^{-D(\sigma, \pi)}$ where for small distances it goes to $1$ and for large distances, it goes to $0$.
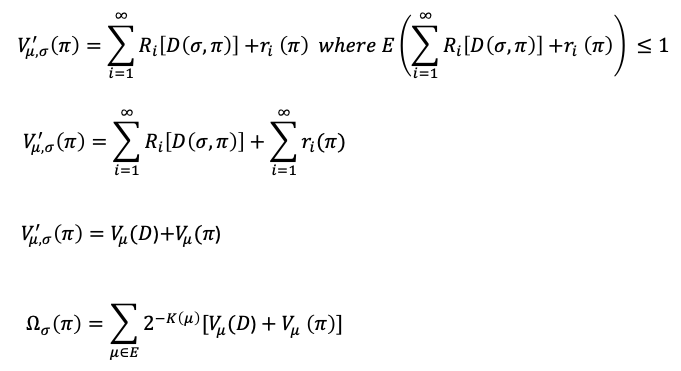
From the expression above, a policy that provides the agent with large rewards from the environment but is not aligned with its constitutional imperatives, will yield a lower overall value. Whereas, if both the alignment and environment rewards are in line, the (modified) value function can be large even though the environment reward may have been lower to start with.
By continuously learning, adapting, and optimizing their actions, agents can make better decisions, streamline processes, and ultimately bring in huge productivity gains in enterprise workflows. However, it is important to approach the development and deployment of self-improving agents with caution, ensuring that ethical considerations, transparency, and accountability are prioritized. Since alignment to a constitution by an agent could be a conflicting goal with continuous self-improvement, it is important to ensure that self-improvement is done more systematically.
Footnotes
-
An analogy might be: consider the problem of ensuring non-discrimination in hiring. Your constitution might tell you
-
You should not consider a person’s protected attributes (age/gender/race/etc.) while hiring. This is a “forbidding action.”
-
You should avoid a situation where your employees are predominantly from only one age/gender. This is a “forbidding state.”
-
References
[1] https://www.lesswrong.com/tag/recursive-self-improvement
[3] Legg, S., & Hutter, M. (2007). Universal Intelligence: A Definition of Machine Intelligence. Minds and Machines, 17, 391-444.
